ロータリーエンジン

icon 項目のみ表示/展開表示の切り替え

ロータリーエンジン　H16.3.13

SVGの代替画像
　 ステーショナリーギアとインナーギアｰの回転している様子です。ステーショナリーギアは固定されています。ロータの位置決めをしています。

エキセントリックシャフトはロータと接している部分については偏心しています。この偏心によってロータの回転が伝わります。エキセントリックシャフトはステーショナリーギアの中を通過しています。ロータ３回転でエキセントリックシャフト１回転

himei.svg

ロータリーエンジンの動き(H16.3.9)

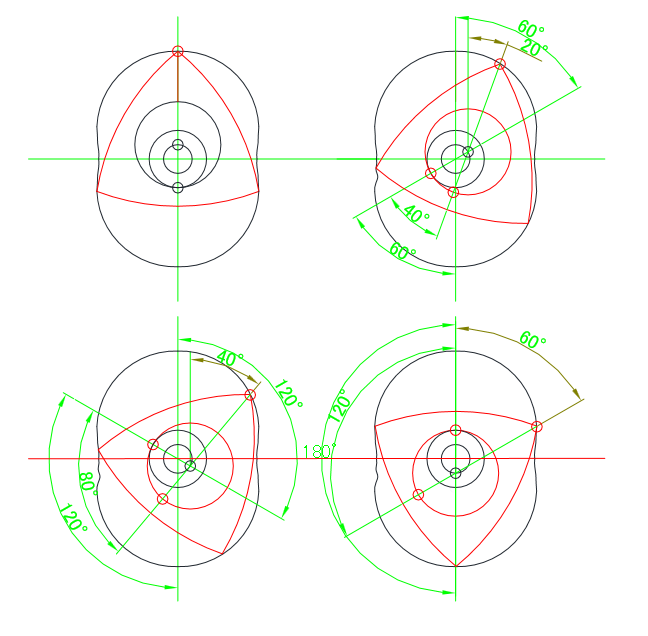
rota3.svg

ロータ等の回転の様子です。動く前の点に○を、動いた後は○をつけました。ロータがロータの中心に対して20度（ロータの中心にたいして）しか回っていないのにエキセントリックシャフトが60度回っているのがわかると思います。また、ロータギアがステーショナリーギアに対して2/3の角度回ること、ロータギアの初期点が動くことがわかります。ロータがエキセントリックシャフトの周りを公転しながら（出力軸の中心から見てステーショナリギアと接している角度の移動量は同じ）自転（ロータの中心からみて公転の1/3ロータが傾く）

　

　

ロータリーハウジングの作図方法(H16.3.13)

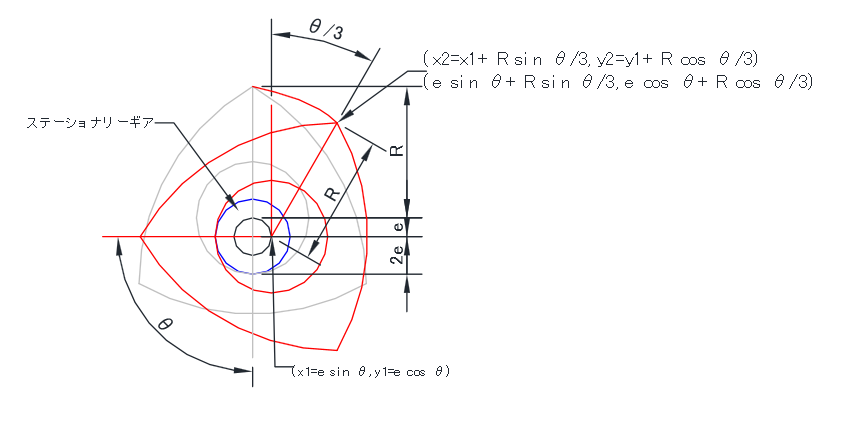
rota_draw.svg

垂直線からステーショナリーギアとインナーギア（ロータの内側の歯）の接点との角度をθとし、ステーショナリーギアの中心の座標を(0,0)とすると

ロータの中心の座標 x1,y1は R sin θ , R cos θ　ロータの天辺の座標　x2,y2は X1+R sin θ,y1+R cos θとなります。

13Bの場合、e=15㎜,ロータリーハウジングの長軸が240㎜、短軸が180㎜なので、R=240/2-15=105㎜となります。ちなみにRX-8の場合、ステーショナリーギアは34歯、ロータギアは51歯です。ロータ幅は80mmです。

θを0度から360度*3まで変化させるとロータリーハウジングが完成します。

一般的に１ロータの排気量といえば、ロータの１辺が、１回転で排出する量で表し13Bの場合、654ccとなっています。

　

Windows上で動作するフリーソフトの「N88互換BASIC Windows」で動作するBASICのソースプログラム r2.bas　実行結果 図-2

　　　　　　　 　　図-2

ロータの作図方法(H16.3.6)図-3

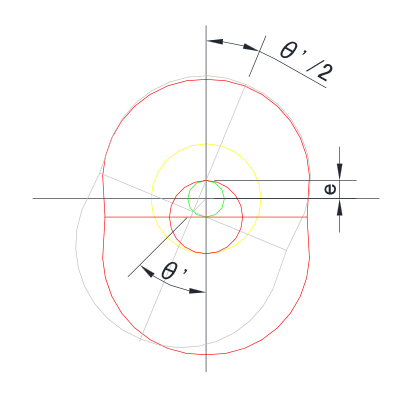
rota_draw2.svg

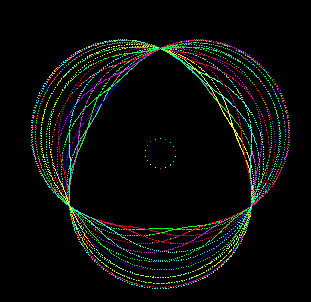
ロータを固定してステーショナリギアをロータの内側の歯車に沿って回すと（ハウジングはステーショナリギアに固定）ハウジングによってロータが描けます。ハウジングを作図するときに、作図する座標をθ'傾け、原点を (e sin θ',e cosθ')ずらせばokです。

座標をθ'傾けるには、ずらす中心を(0,0)とずらしたい点の座標を(x,y)とおけば、ずらした後の座標は(x cos θ' -y sin θ',x sin θ' + y cosθ')となります。

後々の計算を楽に x軸とy軸を入れ替えます。結局ロータの形状は (x,y)=

\displaystyle x= e \cos \theta '+(e \cos \theta +r \cos \frac{\theta}{3})\cos \frac{\theta'}{2}+(e \sin \theta+r \sin \frac{\theta}{3})\sin \frac{\theta'}{2} \displaystyle y= e \sin \theta '-(e \cos \theta +r \cos \frac{\theta}{3})\sin \frac{\theta'}{2}+(e \sin \theta+r \sin \frac{\theta}{3})\cos \frac{\theta'}{2}

であらわせます。

x=

を簡略化すると

展開　 \displaystyle e\cos \theta +e \cos \theta \cos \frac{\theta'}{2}+r \cos \frac{\theta}{3} \cos \frac{\theta'}{2}+e \sin \theta \sin \frac{\theta'}{2}
\displaystyle +r \sin \frac{\theta}{3} \sin \frac{\theta'}{2}
eとrでまとめる e (\cos \theta'+\cos \theta \cos \frac{\theta'}{2}+\sin \theta \sin \frac{\theta'}{2})+r (\cos \frac{\theta}{3} \cos \frac{\theta'}{2}+\sin \frac{\theta}{3} \sin \frac{{\theta}'}{2})
加算公式でまとめる
\displaystyle e (\cos \theta'+\cos( \frac{\theta'}{2}-θ))+r (\cos (\frac{\theta}{3}-\frac{\theta'}{2}))
和差公式でまとめる \displaystyle 2e \cos( \frac{\theta'}{2}+\frac{\theta'}{4}-\frac{\theta}{2}) \cos(\frac{\theta'}{2}-\frac{\theta'}{4}+\frac{\theta}{2})+r \cos(\theta/3-\theta'/2)

整理すると

\displaystyle 2e \cos(\frac{3}{4}*\theta'-\theta*\frac{3}{6})\cos(\frac{1}{4}*\theta'+\frac{\theta}{2})+r \cos(\frac{\theta}{3}-\frac{\theta'}{2})

y=を簡略化すると

展開
\displaystyle y=e \sin \theta'-e \cos\theta \sin \frac{\theta'}{2}-r \cos\frac{\theta}{3} \sin \frac{\theta'}{2}+e \sin\theta \cos \frac{\theta'}{2} +r \sin\frac{\theta}{3} \cos \frac{\theta'}{2}
eとrでまとめる　
\displaystyle y=e(\sin \theta'-\sin \frac{\theta'}{2} \cos \theta+ \cos \frac{\theta'}{2} \sin \theta)+r(-\sin \frac{\theta'}{2} \cos \frac{\theta}{3}+\cos \frac{\theta'}{2} \sin \frac{\theta}{3})
加算公式　
\displaystyle y=e(\sin \theta'+\sin(\theta-\frac{\theta'}{2}))+r \sin(\frac{\theta}{3}-\frac{\theta'}{2})
和差公式
\displaystyle y=2e \sin(\frac{\theta'}{2}+\frac{\theta}{2}-\frac{\theta'}{4}) \cos(\frac{\theta'}{2}-\frac{\theta}{2}+\frac{\theta'}{4})+r \sin(\frac{\theta}{3}-\frac{\theta'}{2})
まとめる　y=2e*sin*(1/4*θ'/2+θ/2)*cos(θ*3'/4-θ/2)+r*sin(-(θ'/2-θ/3))

\displaystyle y=2e \sin(\frac{1}{4}*\frac{\theta'}{2}+\frac{\theta}{2}) \cos(\theta'*\frac{3}{4}-\frac{\theta}{2})+r \sin(-(\frac{\theta'}{2}-\frac{\theta}{3}))

sinとcosの中に式が入ってややこしいのでこれをそれぞれ a bに置きます。

\displaystyle a=\frac{\theta'}{4}+\frac{\theta}{2}
\displaystyle b=\frac{1}{4} θ'-\frac{1}{6}θ
\displaystyle a-b=\frac{\theta}{3}
\displaystyle a=b+\frac{\theta}{3}
\displaystyle b=-\frac{\theta}{3}+a
\displaystyle 3b=\frac{3}{4}*\theta'-\frac{1}{2}\theta
\displaystyle a-b=-\frac{1}{2}\theta'
\displaystyle e:r=1:7
x=2e \cos(3b) \cos(a)+r \cos(2b) y=2e \cos(3b) \sin(a)+r \sin(-2b)

上記のx,yがロータリーの基本形の式です。

ちなみにステーショナリギアとロータギアの比を3:4にすると四角形のロータが 4:5にすると五角形のロータが作図できます。

ロータの原理を作図するプログラム　r3.bas 実行結果 図-3

H16.3.21

左図を表示するC++によるプログラム(ロータが回転します)

ソースファイル

　rota5.cpp(Win32)

　Visual C++ 2013

実行ファイル

　rota5.exe　

ロータリーエンジンの振動特性(H15.5.28)

rota2.svg

　２ロータエンジンは、点火の回数は４気筒エンジンと同じですが、各工程の時間が長いため膨張行程が３個重複しています。よって６気筒エンジンに近い特性になります。ロータリーエンジンはただ単にロータより出力軸の回転数が多いからスムーズというわけではない。それなら変速機で回転数をあげればよいからだ。膨張行程がラップしていること、往復運動をしないことが原因である。