3次方程式の解(Javascript/C++/Excel)

項目のみ表示/展開表示の切り替え

概要

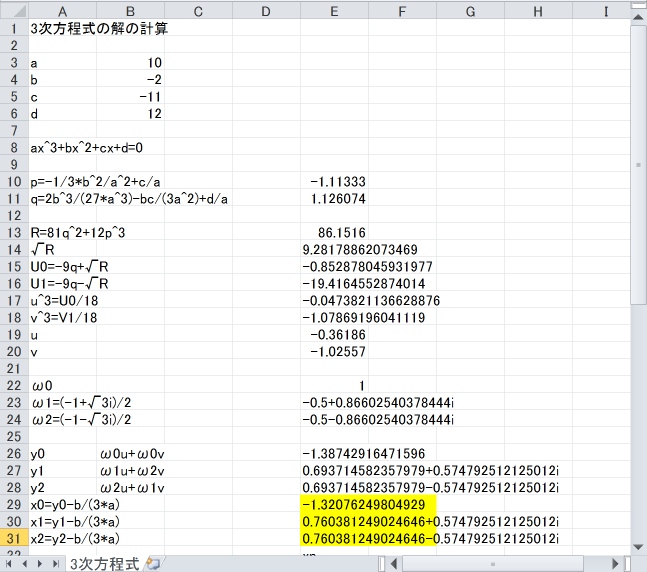
3次方程式の解の導出の算出例の手順に従ってJavascript、C++又はExcelで解を計算する方法を記載します。

JavaScript版

計算例

以下の入力フォームに3次方程式の係数を入力し計算ボタンをクリックすると後述するソースで示すcubic_equation関数を使って解を計算して表示します。
ax^3+bx^2+cx+d=0

cubic_equation関数

上記の式のa～dを引数に指定して呼び出すと複素数を含む解の配列を返します。
例えば

var x=cubic_equation(a,b,c,d);

の様に呼び出した場合x配列は、以下の順番で解が保存されています。

x[0]  1個目の解の実数部
x[1]  1個目の解の虚数部
x[2]  2個目の解の実数部
x[3]  2個目の解の虚数部
x[4]  3個目の解の実数部
x[5]  3個目の解の虚数部

javascriptは複素数をサポートされていないので、虚数が発生する平方根から実数部と虚数部をそれぞれ分けて計算しています。
立方根は虚数を含む場合があるのでアークタンジェントを使用して計算しています。

cubic_equation関数のソースコード

function cubic_equation(a,b,c,d){
  var p=-b*b/3/a/a+c/a;
  var q=2*b*b*b/27/a/a/a-b*c/3/a/a+d/a;
  var r2=81*q*q+12*p*p*p;
  var r_real=0;
  var r_img=0;
  if(r2<0){
    r_img=Math.sqrt(-r2);
  }else{
    r_real=Math.sqrt(r2);
  }
  var u3_real;
  var u3_img
  if(r_img){
    u3_real=-9*q/18;
    u3_img=r_img/18;
    v3_real=-9*q/18;
    v3_img=-r_img/18;
  }else{
    u3_real=(-9*q+r_real)/18;
    u3_img=0/18;
    v3_real=(-9*q-r_real)/18;
    v3_img=0/18;
  }
  var u_real;
  var u_img
  if(u3_img ){
    var z=Math.sqrt(u3_real*u3_real+u3_img*u3_img);
    var t=Math.atan2(u3_img,u3_real);
    z=Math.pow(z,1/3);
    t=t/3;
    u_real=z*Math.cos(t);
    u_img=z*Math.sin(t);
  }else{
    if(u3_real<0)
      u_real=-Math.pow(-u3_real,1/3);
    else
      u_real=Math.pow(u3_real,1/3);
    u_img=0;
  }
  var v_real;
  var v_img
  if(v3_img){
    var z=Math.sqrt(v3_real*v3_real+v3_img*v3_img);
    var t=Math.atan2(v3_img,v3_real);
    z=Math.pow(z,1/3);
    t=t/3;
    v_real=z*Math.cos(t);
    v_img=z*Math.sin(t);
  }else{
    if(v3_real<0)
      v_real=-Math.pow(-v3_real,1/3);
    else
      v_real=Math.pow(v3_real,1/3);
    v_img=0;
  }
  var omega1_real=-0.5;
  var omega1_img=Math.sqrt(3)/2;
  var omega2_real=-0.5;
  var omega2_img=-Math.sqrt(3)/2;
  var y0_real,y0_img;
  var y1_real,y1_img;
  var y2_real,y2_img;
  y0_real=u_real+v_real;
  y0_img=u_img+v_img;
  y1_real=omega1_real*u_real-omega1_img*u_img + omega2_real*v_real-omega2_img*v_img;
  y1_img=omega1_img*u_real+omega1_real*u_img + omega2_img*v_real+omega1_real*v_img
  y2_real=omega2_real*u_real-omega2_img*u_img + omega1_real*v_real-omega1_img*v_img;
  y2_img=omega2_img*u_real+omega2_real*u_img + omega1_img*v_real+omega1_real*v_img

  var x0_real,x0_img;
  var x1_real,x1_img;
  var x2_real,x2_img;
  x0_real=y0_real-b/(3*a);
  x0_img=y0_img;
  x1_real=y1_real-b/(3*a);
  x1_img=y1_img;
  x2_real=y2_real-b/(3*a);
  x2_img=y2_img;
  var x=new Array(6);

  x[0]=x0_real;
  x[1]=x0_img;
  x[2]=x1_real;
  x[3]=x1_img;
  x[4]=x2_real;
  x[5]=x2_img;
  return x;
}

Excel

概要

Excelの複素数の関数を使用して3次方程式の解を計算します。

Excelファイルのダウンロード

ダウンロード cubic_equation.xls(31.5kByte)

C++版

概要

C++のSTLの複素数ライブラリを使用して3次方程式の解を計算します。
コマンドライン上で下記式のa～dの引数を指定し実行すると解を出力します。
ax^3+bx^2+cx+d=0

以下に実行例を示します。

C:>cubic_equation 10 -2 -11 12
10x^3+-2x^2+-11x+12=0
x0=(0.760381,-0.574793)
x1=(-1.32076,-2.77556e-017)
x2=(0.760381,0.574793)

C:>cubic_equation 1 -2 -11 12
1x^3+-2x^2+-11x+12=0
x0=(4,0)
x1=(-3,0)
x2=(1,0)

C:>cubic_equation 1 1 -5 3
1x^3+1x^2+-5x+3=0
x0=(1,0)
x1=(-3,0)
x2=(1,0)

テスト環境

コンパイラ

Visual C++ 2008/2013 Express 32/64bit マルチバイト/UNICODE

実行環境

Windows 7 Enterprise Service Pack 1 64bit Windows 10 Home

プログラムソースの概要

C++のSTLの複素数ライブラリを使用しています。
複素数を標準出力へ出力するのにiostreamを使用しています。iostreamはマルチバイト又はUNICODEで使用可能なTCHAR型をサポートしていないので、マクロでtcout型を定義しています。

_tmain

最初に実行される関数です。
引数の文字列を_tcstod関数により倍精度浮動小数点型に変換します。
解を保存するcomplex<double>型を3個格納する配列xを作成します。
cubic_equation関数にa～dを引数として渡し解を受け取ります。
標準出力toutに解を表示します。

cubic_equation

3次方程式の解を計算します。
立方根を計算するために複素数の指数を計算するpow関数を使用せずにcubic_root関数を呼び出しています。
立方根は複素数を含めると3個の解が存在しますが、意図した解をえるためにcubic_root関数を使用しています。

cubic_root

複素数の立方根を計算します。

プログラムソース

// 3次方程式を解を計算し標準出力に出力(コンソールアプリケーション)

#include <stdio.h>
#include <iostream>
#include <tchar.h>
#include <complex>
#include <math.h>
#include <locale.h>

//      複素数の立方根を計算する

std::complex<double>&  cubic_root(std::complex<double>& y, std::complex<double>& x){
        double z = abs(x);
        z = pow(z, 1.0 / 3.0);
        double t = arg(x)/3.0;
        y = std::complex<double>(z*cos(t), z*sin(t));
        return y;
}

// 3次方程式を解く

void cubic_equation(std::complex<double>* x, double a, double b, double c, double d){
        std::complex<double> A,B3,C,D,E1,E2,T;

        A = std::complex<double>((27.0*a*a*d+2*b*b*b-9*a*b*c)/(54.0*a*a*a), 0);
        double b3=(3.0*a*c-b*b)/(9.0*a*a);
        B3 = std::complex<double>(b3*b3*b3,0);
        C = sqrt(A*A + B3);
        D = std::complex<double>( b/(3.0*a), 0);

        T = -A + C;
        E1 = cubic_root(E1,T);
        T = -A - C;
        E2 = cubic_root(E2, T);

        x[0] = E1+E2-D;
        std::complex<double> W1, W2;

        W1 = (std::complex<double>(-1, 0) + std::complex<double>(sqrt(3.0), 0)*std::complex<double>(0, 1)) / std::complex<double>(2, 0);
        W2 = (std::complex<double>(-1, 0) - std::complex<double>(sqrt(3.0), 0)*std::complex<double>(0, 1)) / std::complex<double>(2, 0);

        x[1] = W1*E1 + W2*E2 - D;
        x[2] = W2*E1 + W1*E2 - D;
}

// 標準出力のTCHAR版を作成
#ifndef tcout
        #ifdef UNICODE
                #define tcout std::wcout
        #else
                #define tcout std::cout
        #endif
#endif

void _tmain(int argc,TCHAR** argv){
        //      UNICODE文字を標準出力に正しく表示させるためにロケールを設定
        _tsetlocale(LC_ALL, _TEXT(""));
        std::complex<double> x[3];
        double a = _tcstod(argv[1],NULL);
        double b = _tcstod(argv[2],NULL);
        double c = _tcstod(argv[3],NULL);
        double d = _tcstod(argv[4],NULL);

        cubic_equation(x, a, b, c, d);

        tcout << a << _TEXT("x^3+") << b << _TEXT("x^2+") << c << _TEXT("x+") << d << _TEXT("=0¥n");
        tcout << _TEXT("x0=") << x[0] << _TEXT("¥n");
        tcout << _TEXT("x1=") << x[1] << _TEXT("¥n");
        tcout << _TEXT("x2=") << x[2] << _TEXT("¥n");
}

ソースコードと実行ファイルのダウンロード

ダウンロード cubic_equation.zip(109kByte)

ZIPファイルに含まれるファイル

cubic_equation.cpp
cubic_equation.exe

ページのトップへ戻る

山本ワールド

Windowsプログラミング