等価回路

入力電圧がVでコンデンサの電荷が0の場合の任意秒後のコンデンサの電圧

入力電圧と各部の電圧

$\displaystyle V=\frac{q}{C}+Rs \cdot (i+iRL)$

$\displaystyle i=\frac{dq}{dt}$

$VRS=Rs \cdot (iRL+i)$

$VC=V-VRS$

$\displaystyle iRL=\frac{q}{C \cdot RL}$

微分方程式に変形すると

$\displaystyle V=\frac{q}{C}+Rs ( iRL + \frac{dq}{dt} )$

$\displaystyle V=\frac{q}{C}+Rs \cdot iRL + Rs \cdot \frac{dq}{dt}$

$\displaystyle V=\frac{q}{C}+Rs \frac{q}{C \cdot RL} + Rs \cdot \frac{dq}{dt}$

微分方程式を解く

過度解

上式のV=0の場合のqtを解きます。

$\displaystyle 0=\frac{q}{C}+Rs \frac{q}{C \cdot RL} + Rs \cdot \frac{dq}{dt}$

$\displaystyle -Rs \cdot \frac{dq}{dt} = \frac{qt}{C}+Rs \frac{qt}{C \cdot RL}$

$\displaystyle \frac{dqt}{dt} = - \frac{qt}{C \cdot Rs}- \frac{qt}{C \cdot RL}$

$\displaystyle \frac{dqt}{dt} = - \frac{qt \cdot RL}{C \cdot Rs \cdot RL}- \frac{q \cdot Rs}{C \cdot Rs \cdot RL}$

$\displaystyle \frac{dqt}{dt} = - \frac{qt ( RL +Rs)}{C \cdot Rs \cdot RL}$

$\displaystyle \frac{dqt}{qt} = - \frac{ RL +Rs}{C \cdot Rs \cdot RL} dt$

両辺を積分する

$\displaystyle \int{ \frac{1}{qt}}dqt = - \frac{ RL +Rs}{C \cdot Rs \cdot RL} \int{ dt }$

$\displaystyle \log_e qt = - t \cdot \frac{ RL +Rs}{C \cdot Rs \cdot RL}+K1$

$\displaystyle qt = \mathrm{e}^{(- t \cdot \frac{ RL +Rs}{C \cdot Rs \cdot RL}+K1)}$

$\displaystyle qt = K \cdot \mathrm{e}^{(- t \cdot \frac{ RL +Rs}{C \cdot Rs \cdot RL})}$

ただし

$\displaystyle K=\mathrm{e}^{K1}$

定常解

定常解のqsは電圧を加えてから無限大の時間が経過した後の値です。すなわちコンデンサに電流が流れないためVをRS+RLで分圧した電圧となる。

$\displaystyle qs=V \frac{RL}{RS+RL}\cdot C$

一般解

一般解は過度解と定常解の和である

$\displaystyle q=qt+qs=K \cdot \mathrm{e}^{(- t \cdot \frac{ RL +Rs}{C \cdot Rs \cdot RL})}+V \frac{RS}{RS+RL}\cdot C$

初期値(K)を決める

t=0,q=0 の時の一般解の式より

$\displaystyle 0=K \cdot \mathrm{e}^{(- 0 \cdot \frac{ RL +Rs}{C \cdot Rs \cdot RL})}+V \frac{RL}{RS+RL}\cdot C$

$\displaystyle 0=K +V \frac{RL}{RS+RL} \cdot C$

$\displaystyle K = -V \frac{RL}{RS+RL} \cdot C$

t秒後のqは下式のとおりとなる

$\displaystyle q=- V \frac{RL}{RS+RL} \cdot C \cdot \mathrm{e}^{(- t \cdot \frac{ RL +Rs}{C \cdot Rs \cdot RL})}+V \frac{RL}{RS+RL} \cdot C$

$\displaystyle q=V \frac{RL}{RS+RL} \cdot C ( 1- \mathrm{e}^{(-\frac{RL+Rs}{C \cdot Rs \cdot RL} \cdot t)})$

Vcは下式より

$q=V \cdot C$

$\displaystyle Vc = V \frac{RL}{RS+RL} ( 1- \mathrm{e}^{(-\frac{RL+Rs}{C \cdot Rs \cdot RL} \cdot t)})$

入力電圧がVでコンデンサの電荷がQの場合の任意秒後のコンデンサの電圧

$\displaystyle q=qt+qs=K \cdot \mathrm{e}^{(- t \cdot \frac{ RL +Rs}{C \cdot Rs \cdot RL})}+V \frac{RL}{RS+RL} \cdot C$

初期のqがQの時

$\displaystyle Q=K \cdot \mathrm{e}^{(- 0 \cdot \frac{ RL +Rs}{C \cdot Rs \cdot RL})}+V \frac{RL}{RS+RL} \cdot C$

$\displaystyle K=Q-V \frac{RL}{RS+RL} \cdot C$

任意秒後のqは下式のとおりとなる

$\displaystyle q=( Q-V \frac{RL}{RS+RL} \cdot C ) \cdot \mathrm{e}^{(- t \cdot \frac{ RL +Rs}{C \cdot Rs \cdot RL})}+V \frac{RL}{RS+RL} \cdot C$

コンデンサの初期電圧からRsとRLで分圧される電圧までの間を、コンデンサとRsとRLが並列に接続された場合の合成抵抗で決まる時定数により変化する。

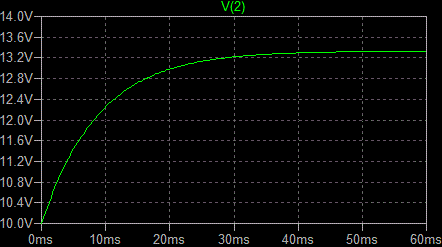
.tran 1us 60ms

vs      1               0       15V

r1      1               2       1
c1      2               0       10000uF IC=10V
r2      2               0       8

.probe
.end