FIR型フィルタの設計
インパルス応答を計算
インパルス応答とは、非常に短い単発の矩形波を入力したときの応答を表します。
周波数応答を逆DFT変換するとインパルス応答が得られます。
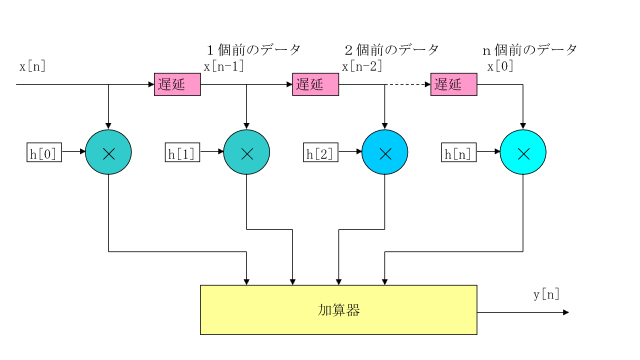
フィルタ係数を得る。
インパルス応答をTAP数分取り出して図のようにシフトさせるとフィルタ係数となります。
使用している係数の数(タップ数)-1がフィルタの次数となります。
カイザー窓
実際には、リップルが生じないように、フィルタ係数にカイザー窓関数を掛け合わせる。
図中のAはdB単位です。
カイザー窓適用後のフィルタ係数は
hh2[n]=hh[n]*wm[n]
窓関数はいろいろなものがあります。
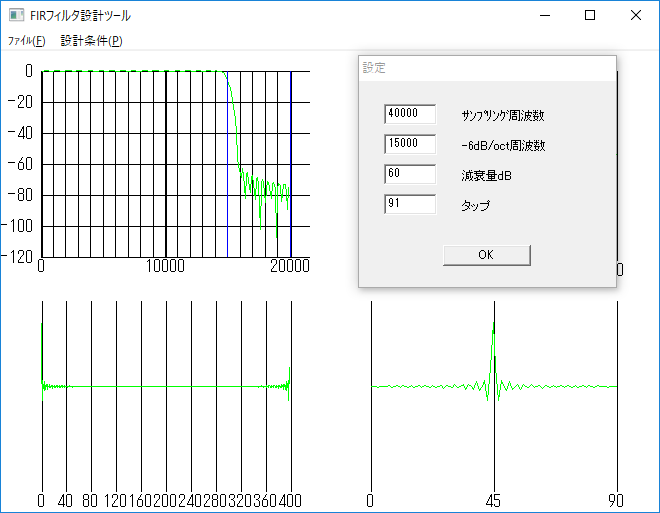
フィルタの周波数特性のチェック
では、設計できたフィルタの周波数特性をチェックしてみましょう。
フィルタ係数をDFT処理すれば、周波数特性が算定できます。

フィルタを設計する簡単なプログラム
Borland C++ 5.5(フリーコマンドライン版)
Visual C++ 5
でコンパイルして実行できました。
H16.12.27版にパラメータの保存機能を追加しました。保存すると実行フォルダにpara.csvファイルが作成されます。
fir.lzh H18.1.2
実行画面
z変換
サンプリングされたデーターがである場合、 z変換は以下のように定義される。
![\displaystyle \sum^{\infty}_{n=\infty}x[n]z^{-n}]()
たとえば、 0,1,2,3,4<>というサンプリングされたデーターがある場合、
![x[0]=0,x[1]=1,x[2]=2,x[3]=3,x[4]=4]()
z 変換すると
![A(z)=1+1Z^{-1}+2Z^{-2}+2Z^{-3}+4Z^{-4}]()