山本ワールド
Windowsプログラミング
アルゴリズム Vitual C++ 2008/2013によるWin32/Win64 APIレベルのプログラム 基礎 Vitual C++ 2008/2013によるAPIレベルのプログラム(32/64bit) Wix3でインストーラーを作る Visual C++ 2008 Standard Editonによるフォームアプリケーションのプログラム(32/64bit) Vitual C++ 2008 Standard EditonによるAPIレベルのプログラム(32/64bit) Windows 7対応 Visual C++ 2008 ExpressによるAPIレベルのプログラム Visual C++ 2005 ExpressによるAPIレベルのプログラム Visual C++ Versiosn 5 BORLAND C++ Windowsプログラム全般 Excel VBA その他マンデルブロ描画プログラム
概要
マンデルブロ描画プログラムVersion2.3
SSE2を使用し2ピクセル同時計算 H26.09.20
SSE2で倍精度浮動小数点を使用し水平方向の2ピクセルを同時計算してみた。
xmmレジスタの上位に1ピクセル目、下位に0ピクセル目を割り当てる。
ソースはインラインアセンブラで記述している。
大まかな概要を以下に示す。
xmmレジスタに格納されているデータについてはnがレジスタ番号とした場合、以下の様に表記する。
倍精度浮動小数点格納時 xmmn xmmnDH xmmnDL
単精度浮動小数点格納時 xmmn xmmn3 xmmn2 xmmn1 xmmn0
movsd命令で引数amax,aminを読み込む。amax,aminは64bitである。xmmレジスタの上位64bitは0でクリアされる。
xmmnH←0,xmmnL←amin
xmmnH←0,xmmnL←amax
xmmdH←xmmdH,xmmdL←xmmdL-xmmsL
xmmnH←xmmnH,xmmnL←32bit整数を倍精度浮動小数点に変換
xmmdH←xmmdH,xmmdL←xmmdL/xmmsL
imm8の0ビット目が0の場合はxmmdLにxmmdLが1の場合はxmmdHがコピーされる。
imm8の1ビット目が0の場合はxmmdHにxmmsLが1の場合はxmmsHがコピーされる。
xmmdH←xmmsL,xmmdL←xmmsL
xmmdH←xmmdH+xmmsL,xmmdL←xmmdL+xmmsL
imm8の0ビット目が0の場合はxmmdLにxmmdLが1の場合はxmmdHがコピーされる。
imm8の1ビット目が0の場合はxmmdHにxmmsLが1の場合はxmmsHがコピーされる。
xmmdH←xmmsL,xmmdL←xmmsH
anH←xmmnH,anL←xmmnL
bmin、bmaxについてもamin、amaxと同様に計算する。
ラベルy_loop
movsd命令でループを抜け出すリミット値をxmmレジスタの下位に読み出す。
shufpd命令でxmmレジスタの上位と下位に下位の値をコピーする。
xorpd命令でxmmレジスタを0クリアすることによりx,y,count値を0クリアする。
ラベルLOOP_L1:
各SSE2命令を使って計算する。
cmpltpd命令でリミット値と比較する。真の場合は64bit全部のビットが1にセットされる。
anH←xmmnH,anL←xmmnL
test命令でedxのビット値が1のビットがあるかチェックする。
jz命令によりedxに1がなければLOOP_L1_EXITラベルへジャンプする。(2ピクセルとも計算が終了したのでループを抜ける。)
movq命令によりxmmの下位64bitに10進数で1を読み込む。
pshufd命令でxmmレジスタの上位と下位に下位の値をコピーする。
cmpltpd命令の結果とpshufd命令の結果をpand命令でAND演算をする。そうするとリミット値を超えていないばあい、整数の1でこれている場合は0となる。
これによりリミット値を超えていない場合はcount値が増えリミット値を超えているとカウント値は増えない。
paddq命令によりpand命令の値とcount値を加算する。
ラベルLOOP_L1にジャンプする。
ラベルLOOP_L1_EXIT
xmmレジスタの上位に1ピクセル目、下位に0ピクセル目のカウント値が保存されているのでこれを色に変換する
メモリ上では1ピクセル4byteで表現しているが、カウント値は64bitなので32bitのみ有効とみなし、shufps命令によりxmmレジスタの0~31bitへxmmレジスタの0~31bitの値、xmmレジスタの32~61bitへxmmレジスタの64~95bitの値をコピーする。
ソースファイル、リソースファイル、実行ファイルダウンロード
マンデルブロ描画プログラム Version 2.00 H26.04.09
Version 1から以下の改良を行いました。
SSEを使用して4ピクセル同時計算を実現
bmpファイル保存ができるように修正
縦の画素数が4の倍数でない場合、マルチスレッドで計算する場合にエラーが発生する点を修正
Visual C++ 2008のUnicode 32bitに移植。アセンブラはMASM向けに変更
各種設定を1つのダイアログボックスにまとめた。
色の割り付けのバグを修正
ベンチマーク用に設定値を初期化できるように修正
計算時間を1秒より小さい単位で測定できるように修正
ソースファイル、リソースファイル、実行ファイルダウンロード
SSEを使用し4ピクセル同時計算 H26.09.20
SSEで単精度浮動小数点を使用し水平方向の4ピクセルを同時計算してみた。
SSEでは128bitのレジスタを8本が使用でき、1つのレジスタには単精度浮動小数点を4個保存できる。
プログラムはインラインアセンブラを使用した。計算部分のみのソースを示す。
FPU版と計算部分の関数は引数が同一なので、置き換えは容易である。
C++版も作成して速度の比較をした。
FPU版とC++版は倍精度、SSE版は単精度なので単純比較はできないが、それでもSSE版は高速である。
FPUとC++では優位な速度差がない。C++でも十分な速度がでるので、FPUの優位性が感じられない。
計算条件 800*600ピクセル a=-1.3333~1.3333 b=-1.0~1.0 反復回数最大32768
各CPUの演算性能
各世代のCPUでフラクタルを1スレッドで実行した場合の速度をクロックに影響されないように1GHzに換算してみた。値が小さいほど高速である。Pentium4の遅さが目立つ。他のCPUでは1GHzあたりで換算すると速度はほぼ同一である。i3-370MについてはOSをバージョンアップしたので再度測定した。(H26.09.20)
| CPU | clock | FPU | SSE |
|---|---|---|---|
| i5-3230M | 2.6GHz(3.2GHz) | 79 | 17 |
| i7-3820 | 3.6GHz(4.2GHz) | 64 | 15 |
| i7-2600 | 3.6GHz(3.8GHz) | 64 | 15 |
| i3-370M | 2.4GHz | 63 | 15 |
| i7-870 | 2.93GHz(3.6GHz) | 63 | 15 |
| Core2Duo E7500 | 2.93GHz | 67 | 17 |
| Core2Duo E6320 | 1.86GHz | 66 | 18 |
| Pentium4 641 | 3.2GHz | 162 | 37 |
i5-3230M(2.6GHz) Ivy Bridge
| CPU | C++ | FPU | SSE | 速度比(FPU/SSE) |
|---|---|---|---|---|
| 1スレッド | 24.445 | 24.835 | 5.45 | 4.56 |
| 2スレッド | 12.23 | 12.496 | 2.745 | 4.55 |
| 4スレッド | 10.483 | 10.967 | 2.636 | 4.16 |
| 8スレッド | 8.097 | 9.485 | 2.606 | 3.64 |
| 16スレッド | 7.082 | 8.205 | 2.309 | 3.55 |
| 32スレッド | 6.864 | 7.987 | 2.294 | 3.48 |
i7-3820(オーバークロック4.2GHz) Sandy Bridge-E
| CPU | C++ | FPU | SSE | SSE2 | 速度比(FPU/SSE) |
|---|---|---|---|---|---|
| 1スレッド | 15.078 | 15.295 | 3.637 | 12.906 | 4.205 |
| 2スレッド | 7.609 | 7.769 | 1.846 | 6.766 | 4.209 |
| 4スレッド | 6.339 | 6.568 | 1.607 | 3.160 | 4.087 |
| 8スレッド | 4.100 | 4.309 | 1.077 | 2.155 | 4.001 |
i7-2600(3.8GHz) Sandy Bridge
| CPU | C++ | FPU | SSE | SSE2 | 速度比(FPU/SSE) |
|---|---|---|---|---|---|
| 1スレッド | 17.082 | 17.082 | 4.056 | 7.972 | 4.146 |
| 2スレッド | 8.643 | 8.783 | 2.106 | 4.13 | 4.104 |
| 4スレッド | 7.269 | 7.473 | 1.763 | 3.620 | 4.123 |
| 8スレッド | 4.648 | 4.852 | 1.201 | 2.340 | 3.870 |
i3-370M(2.40GHz) Arrandale
| CPU | FPU | SSE | SSE2 | 速度比(FPU/SSE) |
|---|---|---|---|---|
| 1スレッド | 26.094 | 6.359 | 12.906 | 4.103 |
| 2スレッド | 14.485 | 3.312 | 6.766 | 4.373 |
| 4スレッド | 12.672 | 2.984 | 6.281 | 4.247 |
| 8スレッド | 11.000 | 2.688 | 5.547 | 4.092 |
i7-870(2.93GHz) Lynnfield
| CPU | FPU | SSE | 速度比(FPU/SSE) |
|---|---|---|---|
| 1スレッド | 17.582 | 4.228 | 4.158 |
| 2スレッド | 9.22 | 2.231 | 4.133 |
| 4スレッド | 8.003 | 1.95 | 4.104 |
| 8スレッド | 5.741 | 1.451 | 3.957 |
Core2Duo E7500(2.93GHz) Wolfdale
| CPU | FPU | SSE | C++ | 速度比(FPU/SSE) |
|---|---|---|---|---|
| 1スレッド | 22.745 | 5.96 | 23.868 | 3.82 |
| 2スレッド | 11.42 | 3.011 | 11.981 | 3.79 |
| 4スレッド | 11.388 | 3.526 | 11.95 | 3.22 |
| 8スレッド | 11.622 | 2.995 | 12.18 | 3.88 |
Core2Duo E6320(1.86GHz) Conroe
| CPU | FPU | SSE | C++ | 速度比(FPU/SSE) |
|---|---|---|---|---|
| 1スレッド | 35.75 | 9.438 | 37.109 | 3.788 |
| 2スレッド | 17.984 | 4.75 | 18.671 | 3.786 |
| 4スレッド | 17.953 | 4.75 | 18.594 | 3.776 |
| 8スレッド | 18.11 | 4.766 | 18.641 | 3.800 |
Pentium4 641(3.2GHz) Cedar Mill
| CPU | FPU | SSE | SSE2 | 速度比(FPU/SSE) |
|---|---|---|---|---|
| 1スレッド | 50.64 | 11.625 | 19.875 | 4.356 |
| 2スレッド | 27.078 | 7.375 | 14.375 | 3.687 |
| 4スレッド | 26.938 | 7.422 | 14.438 | 3.629 |
| 8スレッド | 26.828 | 7.39 | 14.406 | 3.630 |
SSE版のソースコード
// SSEを使用し水平4ピクセルを同時フラクタル計算を実行
void mandel_draw_sse(double a1,double b1,double a2,double b2,int sx,int sy,BYTE* pBits){
float amax=(float)a2;
float amin=(float)a1;
int scrx=sx;
float bmax=(float)b2;
float bmin=(float)b1;
int scry=sy;
BYTE* p=pBits;
const float lim=4.0;
const unsigned B_MASK=0x0000c0;
const unsigned B8_MASK=0x0000e0;
const unsigned B32_MASK=0x0000f8;
const unsigned CONST1=1;
__m128 an;
__m128 astep;
__m128 bn;
__m128 bstep;
_asm{
mov eax,p
mov edi,scry
mov esi,scrx
movss xmm1,amax
movss xmm0,amin
subss xmm1,xmm0
cvtsi2ss xmm2,esi
divss xmm1,xmm2 ; astep
shufps xmm0,xmm0,0x34 ; 3<-0 2<-2 1<-1 0<-0
addss xmm0,xmm1
shufps xmm0,xmm0,0xc4 ; 3<-3 2<-0 1<-1 0<-0
addss xmm0,xmm1
shufps xmm0,xmm0,0xe0 ; 3<-3 2<-2 1<-0 0<-0
addss xmm0,xmm1
shufps xmm0,xmm0,0x1b ; 3<-0 2<-1 1<-2 0<-3
shufps xmm1,xmm1,0 ;
movaps an,xmm0
addps xmm1,xmm1
addps xmm1,xmm1
movaps astep,xmm1
movss xmm3,bmin
movss xmm2,bmax
subss xmm3,xmm2
cvtsi2ss xmm4,edi
divss xmm3,xmm4 ; bstep
shufps xmm2,xmm2,0x34 ; 3<-0 2<-2 1<-1 0<-0
addss xmm2,xmm3
shufps xmm2,xmm2,0xc4 ; 3<-3 2<-0 1<-1 0<-0
addss xmm2,xmm3
shufps xmm2,xmm2,0xe0 ; 3<-3 2<-2 1<-0 0<-0
addss xmm2,xmm3
shufps xmm2,xmm2,0x1b ; 3<-0 2<-1 1<-2 0<-3
shufps xmm3,xmm3,0 ;
movaps bn,xmm2
movaps bstep,xmm3
y_loop:
mov esi,scrx
shr esi,1
shr esi,1
movups xmm0,an
x_loop:
movss xmm7,lim
shufps xmm7,xmm7,0
xorps xmm4,xmm4 ; x=0
xorps xmm5,xmm5 ; y=0
xorpd xmm1,xmm1 ; count
mov ecx,loop_n_max
LOOP_L1:
movaps xmm6,xmm4
mulps xmm6,xmm5 ; x*y
addps xmm6,xmm6 ; 2*x*y
subps xmm6,xmm2 ; zy=2*x*y-b
mulps xmm4,xmm4 ; x2=x*x
mulps xmm5,xmm5 ; y2=y*y
movaps xmm3,xmm4
subps xmm4,xmm5 ; x2-y2
subps xmm4,xmm0 ; x=zx=x2-y2-a
addps xmm3,xmm5 ; x2+y2
movaps xmm5,xmm6 ; y=zy
cmpltps xmm3,xmm7 ; x2+y2<4 真 1 偽 0
pmovmskb edx,xmm3 ; 各バイトの最上位ビットをedxにコピー
test edx,edx ; 4ピクセルがともにlimを超えた場合ループを抜ける
jz LOOP_L1_EXIT
movd xmm6,CONST1
pshufd xmm6,xmm6,0
pand xmm3,xmm6
paddd xmm1,xmm3 ; 前の比較命令が真の時カウントされる
loop LOOP_L1
LOOP_L1_EXIT:
; RR RRRG GGGGB BBBB->RRRR R000 GGGG G000 BBBB B000 32768色を32bitカラーにマッピング
movdqa xmm5,xmm1 ; 00RR RRRB BBBB
pslld xmm1,3 ; R RRRR BBBB B000
movdqa xmm4,xmm1
movd xmm7,B32_MASK
shufps xmm7,xmm7,0
pand xmm1,xmm7 ; 青
; 000G GGGG 0000 0000
pslld xmm4,3 ; GGGG G000 0000 0000
movdqa xmm5,xmm4
pslldq xmm7,1
pand xmm4,xmm7 ; 緑
por xmm1,xmm4
; 000R RRRR 0000 0000 0000 0000
pslld xmm5,3 ; RRRR R000 0000 0000 0000 0000
pslldq xmm7,1
pand xmm5,xmm7 ; 赤
por xmm1,xmm5
movups [eax],xmm1
add eax,16
movaps xmm1,astep
addps xmm0,xmm1 ;an+=astep
dec esi
jnz x_loop
movups xmm3,bstep
addps xmm2,xmm3
dec edi
jnz y_loop
}
}
C++版のソースコード
void mandel_draw_c(double a1,double b1,double a2,double b2,int sx,int sy,BYTE* pBits){
int x0=sx;
int y0=sy;
double a_min=a1;
double a_max=a2;
double b_min=b1;
double b_max=b2;
double a_step=(a_max-a_min)/x0;
double b_step=(b_max-b_min)/y0;
BYTE* top=pBits;
double b=b_max;
while(y0--){
double a=a_min;
x0=sx;
while(x0--){
double x=0;
double y=0;
unsigned int c=0;
for(c=0 ; c < ::loop_n_max ; c++){
double x2=x*x;
double y2=y*y;
double zx=x2-y2-a;
double zy=2*x*y-b;
x=zx;
y=zy;
if(x2+y2>= ::LOOP_MAX)
break;
}
unsigned cr,cg,cb;
switch(color_max){
case 32768: // 0rrr rrgg gggb bbbb
cr=(c<<3) & 0xf8;
cg=(c>>2) & 0xf8;
cb=(c>>6) & 0xf8;
c=RGB(cr,cg,cb);
break;
case 4096: // rrrr gggg bbbb
cr=(c<<4) & 0xf0;
cg=c & 0xf0;
cb=(c>>4) & 0xf0;
c=RGB(cr,cg,cb);
break;
case 512: // r rrgg gbbb
cr=(c<<5) & 0xe0;
cg=(c<<2) & 0xe0;
cb=(c>>1) & 0xe0;
c=RGB(cr,cg,cb);
break;
case 64: // rr ggbb
cr=(c<<2) & 0xc0;
cg=(c<<4) & 0xc0;
cb=(c<<6) & 0xc0;
c=RGB(cr,cg,cb);
break;
}
INT32* i32=(INT32*)pBits;
*i32=c;
pBits+=sizeof(INT32)/sizeof(pBits[0]);
a+=a_step;
}
b-=b_step;
}
}
色の割り付けのバグ H24.5.6
64色の場合、赤色が描画に反映されないことを発見した。すなわち実際は、16色表示となっていた。
色は、RGB形式で割り付けているため、大半がループの回数が少ない場合、特定の色に偏り面白みがない。
色の割り付けについては、再度見直し予定である。
コンパイラでのSSE命令 H24.5.6
アセンブラでFPUを使った場合とC++で記述し、コンパイラでSSE命令を吐き出させた場合で速度を比較するとほぼ同等でした。
Version 1.00 H17.12.23
主要計算ルーチンにインラインアセンブラを使用しFPUを酷使した、マンデルブロ描画プログラムを作成しました。
H17.04.10 公開
H17.04.19 描画をDIB上にするように変更。ファイルへ保存できるように変更。
特徴
FPUをアセンブラレベルで使用することにより高速化を果たしている。
画面上でマウスにより任意の範囲を拡大したり、中心点を移動することが可能。
ディスクトップサイズにとらわれず大きな画像を作成可能。8192*8192の画像が作成できました。
画像をクリップボードへコピーできる。
BMP形式で保存できる。
マルチモニターが使える場合は、その大きさに合わせて画像を作成したり、ウィンドウの大きさをあわせることが可能。
概要
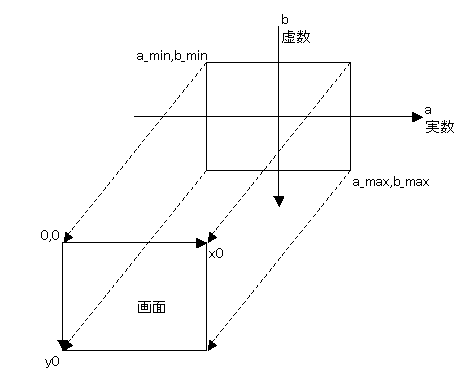
マンデルブロについて
Zn+1=Zn2+C
Z= x+yiC=a+biとした場合でZ=Z^2+C が成り立つ場合のxとyを求めます。
xn+1+yn+1i=(xn+yni)^2+a+bi → xn+1+yn+1i=xn^2+2*xn*yni-yn^2+a+bi
実数: xn+1=xn^2-yn^2+a
虚数: yn+1=2*xn*yn+b
|
この式を簡単に解けないためx0=0,y0=0からスタートして近似していいきます。このときの近似回数をその点の色とします。ただし、Zの絶対値√(x^2+y^2)が2を超えた場合、発散して近時できないので打ち切りとし黒とします。また、近似回数の上限値を超えた場合、黒とします。
これらの計算を画面の横方向X座標をaとし縦方向をY座標をbとしてそれぞれの色を求めてます。 |
下記は原始的なプログラムです。
void draw(HDC hdc,double x0,double y0){
double a_min=-0.7;
double a_max=1.5;
double b_min=-1.5;
double b_max=1.5;
double a_step=(a_max-a_min)/x0;
double b_step=(b_max-b_min)/y0;
int wx,wy;
wx=
0;for(doublea=a_min;a<=a_max;a+=a_step){
wy=
0;for(doubleb=b_min;b<=b_max;b+=b_step){
double x=0;
double y=0;
int c=
0;for(c=0;c<=511;c++){
double x2=x*x;
double y2=y*y;
double zx=x2-y2-a;
double zy=2*x*y-b;
x=zx;
y=zy;
if(x2+y2>=4)
break;
}
if(c==512){
c=0;
SetPixel(hdc,wx,wy,0);
}else{
SetPixel(hdc,wx,wy,color_map512(c));
}
++wy;
}
++wx;
}
}
本プログラムでは、作成したい画像サイズに合わせたバッファをメモリ上に確保し、上記のC++のコードをアセンブラでコーティングされたルーチンにてメモリ上に描画します。
その後、表示の更新が生じた場合に、絶えずウィンドサイズに作成した画像全体が表示されるように拡大縮小して表示します。
メモリ上では32bitカラーで扱っており、8192*8192程度の大きさのサイズが限界でした。これを16bitにすればもっと大きな画像も作成できるでしょう。
アセンブラで作成したルーチンは内部でグローバル変数を変更せず、しかも内部で関数等を呼び出していないため、HT対応のPentium4やXeonのDualにあわせてスレッド数を増やすこともできるでしょう。
メニュー
|
名前をつけて保存 | 画像をbmp形式でファイルに保存する。 |
| 終了 | 本プログラムを終了する。 |
| コピー | クリップボードへ画像をコピーする。 |
|
前に戻る | 直前の画像を表示する |
| 次に進む | 直後の画像を表示する | |
| 反復回数 | 計算の打ち切り回数を指定 | |
| 色数 | 収束回数を何色に割り当てるか指定 | |
| フラクタル座標設定 | 表示するフラクタル座標範囲を数字で指定 | |
| 窓ズーム | 表示画面上で拡大する領域を指定する。 | |
| 移動 | 表示画面上でどこを中心にするか指定 | |
| ズームアウト | 表示画面を0.5倍にする。 | |
| イメージサイズ 任意 | 任意のイメージサイズの画像に設定する | |
| イメージサイズ | ディスクトップの大きさの画像に設定する。マルチモニタの場合プライマリモニターの大きさとなる。 | |
| イメージサイズ | マルチモニタをサポートしている場合に表示される。全マルチモニターの合成サイズの大きさの画像に設定する。 | |
| マルチモニター全体で最大化 | マルチモニタをサポートしている場合に表示される。全マルチモニターの合成サイズの大きさにウィンドウサイズをあわせる。 |
プログラムはVisual C++ 5.0で作成されています。Windows NT 4.0 、Windows 2000、Windows XPで動作確認しました。
当初Visual C++ 5.0のインラインアセンブラで記述していましたが、nasm用に変更しました。かなり文法が異なっているように思いました。ちなみに800*600の画像サイズで -1.333,-1.000 1.333,1.000の領域 反復回数の上限を32768とした場合の計算時間は、下記のとおりです。ウィルスバスターやLAN等につながった状態なのであまり正確ではありませんが
Thknkpad240X PentiumⅢ 500MHz RAM 192MBytes HDD 10GB Windows 2000 Professional 224秒 Pentium4比で考えれば意外に検討しているような気がする。
Pentium4 3.2G(Prescot Dステップ Socket 478) RAM 1GBytes(デュアルチャンネル) HDD 120GB Windows XP Professional 51秒
Pentium2 350MHz(Deschutes) RAM 128MBytes HDD 5GB Windows NT 4.0 Server 303秒
Pentium M 1.6GHz RAM 256MB Windows 2000 Professional 50秒
Pentium4を上回るスコア、Pentium4のFPUは1/2のクロックで動作している。
Athlon64 3000+(Socket 939) RAM 1GHz Windows 2000 Professional 41秒
Pentium 4 を上回るスコア。伝統的にFPUが強いのが裏付けられた。
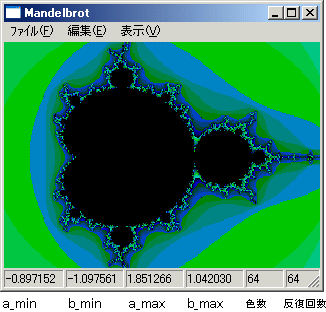
Version 1.01 H18.05.07
ハイパースレッドの威力を試したくてアセンブラで記述された関数を2スレッド以上起動できるように改造した。
スレッド数は、表示メニューから選びます。
Pentium IV 3.2GHz(Prescot Socket 478)で2スレッドにすると51秒が26秒にスピードアップした。スレッド数増加によるオーバーヘッドは8スレッド程度ではPentium IV、Athlon64 3000+では見られなかった。
ATOM N280での実行速度 H21.5.31
ATOM N280(1.66GHz)で実行したところ 1スレッドで193秒、2スレッドで109秒であった。いずれにしてもFPUは今後、互換性のためだけに使われる運命のためあまり比較する意味はない。
実行速度 2014.01.19
i7-3820とi7-2600では同じ4コア8スレッドでコアの世代もSandy Bridgeである。実行速度を比べるとi7-3820では倍ほどの速度が出ている。ためしにi7-3820をクワッドチャンネルからデュアルチャンネル更にシングルチャンネルに変更しても速度は変わらなかった。キャッシュの違いであろうか。
LynnfieldやHaswellやSandy Bridgeともに4コアの場合2スレッドから4スレッドでの速度の伸びが少ないが8スレッドにすると速くなる。4コアでHT無でも同様である。2コアでHTの場合は8スレッド時の伸びが悪くなる。
| CPU | clock | 1スレッド | 2スレッド | 4スレッド | 8スレッド | L2 | L3 | メモリ |
|---|---|---|---|---|---|---|---|---|
| i5-3230M (Ivy Bridge) | 2.6GHz | 25 | 12 | 11 | 10 | 256k*2 | 3MB | |
| i7-3770 (Ivy Bridge) | 3.4GHz | 17 | 8 | 7 | 5 | 256k*4 | 8MB | デュアルチャンネルPC3-12800 11-11-11-28(800MHz) |
| i7-870 (Lannfield) | 2.9GHz | 21 | 10 | 9 | 6 | 256k*4 | 8MB | デュアルチャンネルメモリPC3-10700 9-9-9-24(667MHz) |
| i7-860 (Lannfield) | 2.8GHz | 19 | 9 | 8 | 7 | 256k*4 | 8MB | デュアルチャンネルメモリPC3-10700 9-9-9-24(667MHz) |
| i7-4770 (Haswell) | 3.4GHz | 17 | 9 | 8 | 5 | 256k*4 | 8MB | シングルチャンネルメモリPC3-12800 11-11-11-28(800MHz) |
| i7-3820 (Sandy Bridge-E) | 3.6GHz | 10(Turbo Boost 4.2GHz) | 5(Turbo Boost 4.2GHz) | 4(Turbo Boost 4.2GHz) | 3(Turbo Boost 4.2GHz) | 256k*4 | 10MB | クワッドチャンネルメモリPC3-12800 11-11-11-28(800MHz) |
| i7-2600 (Sandy Bridge) | 3.4GHz | 17 | 9 | 8 | 6 | 256k*4 | 8MB | シングルチャンネルメモリ PC3-10700 9-9-9-24(667MHz) |
| i7-2600 (Sandy Bridge) | 3.4GHz | 17 | 9 | 7 | 5 | 256k*4 | 8MB | デュアルチャンネルメモリ PC3-10700*2(667MHz) |
| i5-2500 3.3GHz 2.66GHz (Sandy Bridge) | 3.3GHz(Turbo Boost on) | 18(25%) | 10(50%) | 8(50%) | 5(100%) | 256k*4 | 6MB | デュアルチャンネルメモリPC-10600 CL9(667MHz) |
| Core i3-2100 (Sandy Bridge) | 3.1GHz | 21 | 10 | 10 | 8 | 256k*2 | 3MB | シングルチャンネルメモリPC-10600 9-9-9-24(667MHz) |
| i3-370M (Arrandale) | 2.4GHz | 26 | 14 | 13 | 13 | 256kB*2 | 3MB | デュアルチャンネルメモリ PC3-8500 8-8-8-19 |
| i5-750 2.66GHz (Lynnfield) | 2.8GHz(ターボブース時) | 22 | 11 | 9 | 6 | 256kB*4 | 8MB | デュアルチャンネルメモリ PC-10600(667MHz) |
| Core2 Q8200 (Yorkfield) | 2.33GHz | 29 | 14 | 12 | 8 | 2M*2 | デュアルチャンネルメモリ PC2-6400 6-6-6-18(400MHz) | |
| Core 2 Duo E6850(Conroe) | 3.0GHz | 23 | 13 | 12 | 12 | 4MB | デュアルチャンネルメモリPC2-6400 5-5-5-16(400MHz) | |
| Core 2 Duo E4500 (Conroe) | 2.2GHz(FSB 800MHZ) | 30 | 15(100%) | 16 | 15 | 2MB | ||
| Core 2 Duo E4300 (Conroe) | 1.8GHz | 37 | 19 | 19 | 19 | 2MB | デュアルチャンネルメモリPC2-5300 5-5-5-15(333MHz) | |
| Celeron 450 (Conroe-L) | 2.2GHz | 31 | 30 | 31 | 31 | 512k | シングルチャンネルメモリ PC3-10700 6-6-6-15(400MHz) | |
| Pentium D 945 (Presler) | 3.4GHz | 26(50%) | 13(100%) | 14 | 14 | 2M*2 | デュアルチャンネルメモリPC2-6400 6-6-6-18(400MHz) | |
| Pentium 4 641 (Cedar Mill) | 3.2GHz | 51 | 27 | 27 | 27 | 2M | デュアルチャンネルメモリPC2-4300 4-4-4-12(266MHz) | |
| Pentium 4 531 (Prescott) | 3.0GHz | 54(50%) | 29(100%) | 29 | 29 | 1M | シングルチャンネルメモリPC2-4300 4-4-4-12(266MHz) | |
| Pentium IV FSB800MHz (Prescott Socket478) | 3.2GHz | 51 | 26 | 1MB | デュアルチャンネルメモリPC3200(400MHz) | |||
| ATOM N280 FSB667MHz (Diamondville) | 1.66GHz | 193 | 109 | 512kB | ||||
| ATOM D525 (Pineview) | 1.8GHz | 134 | 69 | 58 | 41 | 1MB | ||
| PentiumIII FSB100MHz (Coppermine) | 500MHz | 224 | 250kB | |||||
| PentiumII FSB100MHz (Deschutes) | 350MHz | 303 | 512kB | |||||
| Pentium M FSB400MHz (Banias) | 1.6GHz | 50 | 1MB | |||||
| Athlon64 3000+ (Venice) | 1.8GHz | 41 | 512kB | デュアルチャンネルメモリPC3200(400MHz) |
i5-750はクワッドコアでハイパースレッド無であるが、4スレッド以上もスピードが上がっている。4スレッド時のCPUの使用率は50%である。
同様にD525は2スレッドであるがハイパースレッドがあるため論理4CPUである。が8スレッドの方がスピードが速い。何らかの待ちにより100%性能を発揮できないため、スレッド数を増やすことによりさらに性能を増やすことができる。
